knn 搜索的终极加速方法，从此算力不再虚标！

by ·knn 搜索的终极加速方法，从此算力不再虚标！已关闭评论

knn 搜索的终极加速方法，从此算力不再虚标！

作者：hws000（hws.000#163.com）
声明：版权所有，转载请联系作者。
出处：https://blog.simbot.net/2023/03/03/knn_search_acceleration_method/

摘要

        本文创造性的提出一种新的knn（k nearest neighbor）搜索加速算法，可以让硬件的利用率达到90%以上。本算法将knn搜索从计算密集、内存IO密集算法，改进为纯计算密集算法，充分挖掘硬件能力，只要堆更多的硬件，就能实现更快的计算。新算法不但可以运行在GPU上，还可以高效运行于各种专业矩阵加速卡上。

1.引言

        knn搜索是精确搜索，通常作为复杂算法的基础，如knn图构建[6]、聚类算法（如k-means）等。这些算法常用于人脸识别[2]、图像搜索[3]、数据挖掘等场景。knn搜索中有两种常用的距离计算方式：内积、欧式距离。在批量计算时，查询数据表示为M，数据库数据表示为N，数据维度表示为K，内积距离计算方法即MN，此公式与矩阵乘等价；欧式距离的计算方法为Mnorm+Nnorm-2MN，可以变换为2(Mnorm/2+Nnorm/2-MN)，Mnorm/2和Nnorm/2可以提前计算并作为常量数据读取，此公式等同于矩阵乘和三元加。因此两种距离计算方式均可通过矩阵乘法加速。knn搜索数据集的维度通常介于96～512之间，很少有数据集能超过512的维度。Jia Zhe等人分析了矩阵乘法在NVidia Turing T4 GPU上的执行效率[1]，在K比较低时，随着K值增大计算效率逐渐升高。硬件的计算能力是固定的，为什么不同的K值会表现出不同的计算效率？主要问题出在结果的输出上，相同的计算量（即2MNK），不同的K会产生不同的结果个数，内存带宽瓶颈导致K值比较低时，计算结果不能及时输出。knn搜索不仅要计算距离，还要对距离进行排序，才能最终得到TopK个结果，而排序必定需要再次读取计算结果，使内存带宽的瓶颈被进一步放大。Jeff Johnson等人将GPU用于向量搜索[6]时，GPU算力远低于现在，内存带宽的问题并不明显，但TensorCore出现以后，GPU算力直接提升数倍，而内存带宽的提升却有限。我们提出一种计算距离并立即过滤的复合函数，在K值较低时也可以有很高的计算效率，并使用很低的内存带宽，而且能对过滤结果的数量进行控制，从而提高排序性能。

本文作出了以下贡献：
提出一种计算距离并立即过滤的复合函数，只输出符合过滤条件的结果，减少对内存带宽的依赖；
设计一套高效的更新过滤阈值的方法，保证过滤结果准确、可控，同时减少排序的计算量；
针对维度较低的数据，提出一种让查询数据常驻寄存器的方法，进一步提升硬件利用率。

2.研究方法

算力与内存带宽

        在进行内积距离的knn搜索时，假设每次处理的查询量为M条，数据库的数据量为N条，数据维度为K，距离的计算量为2MNK FLOPS，输入、输出类型均为half（FP16 占用2字节），结果输出为2MN字节，输入数据为2(MK+NK)字节。当M远大于K，并远小于N时，输入数据远小于输出数据，内存读写量近似为2MN字节。即当计算量为2MNK FLOPS 时，内存读写量为2MN字节。RTX 2080ti的内存带宽为0.6TB/s，当K为128时，只需76.8TFLOPS的算力就可以产生0.6TB的结果(0.6×128=76.8)，而2080ti的理论算力是107.6，此时的硬件利用率为71.4%。数据库的数据规模N一般都在百万以上，knn搜索时TopK的取值一般在1～128之间，使得TopK远小于N。因为大多数距离计算结果不会出现在最终的搜索结果里，所以对距离计算结果进行过滤，可以大大减小输出的字节数。

阈值的产生与更新

        假设数据是随机分布的，搜索结果也会近似均匀的分散在N中。可以将N分为多段，逐段搜索，并使每个分段大小均等于已经搜索的数据量。当N为131072，TopK为128时，分段大小n可以设为以下值：

分段 0 1 2 3 4 5 6 7 8
n 512 512 1024 2048 4096 8192 16384 32768 65536

表1

        处理分段0时，没有过滤阈值，对n条数据进行距离计算、排序，保存前TopK个结果，将最后一个结果的距离值设置为阈值T。处理分段1～S时，使用阈值T对距离计算结果进行过滤，将新过滤的结果与旧的结果合并、排序，用第TopK个结果的距离值更新阈值T，重复此步骤，直到所有数据处理完毕。由于搜索结果分布均匀，前n次过滤得到TopK个结果，再过滤n次，结果个数也应该跟TopK接近。因为过滤的结果数不会完全等于TopK，可能会大于，也可能会小于，并且需要保留上次排序的结果，所以结果的存储空间应该大于2TopK，如设置为4TopK。

        由于每个分段均可过滤出TopK个结果，依次处理完所有分段才能得到最终结果，造成排序负担较重。在实际使用时，可以在初期使用较少的过滤目标数，并逐步增加到TopK。当TopK为512时，过滤目标数、获取阈值T的位置等参数可以使用表2中的值。其中分段4、6、8、10与分段3、5、7、9的目标数相同，属于矫正分段，是为了防止上一个分段没有过滤出目标数量的结果，导致过滤阈值T持续不更新。为了获得更快的排序效果，可以进一步减少矫正分段的比例。

分段 0 1 2 3 4 5 6 7 8 9 10
n 128 128 256 512 1024 2048 4096 8192 16384 32768 65536
目标数 — 32 32 64 64 128 128 256 256 512 512
T位置 32 32 64 64 128 128 256 256 512 512 —

表2

需要注意的是：为确保数据随机分布，可能要预先随机调换每条数据的存放位置，否则会导致过滤出的结果数不可控。

查询数据常驻寄存器

        在CUTLASS介绍[8]和mma指令文档[11]中，详细说明了TensorCore的使用方式。一条mma指令需要整个warp中的32个thread协作完成，每4个thread成为一组，每组thread的数据组合为一个m或n，共分为8组，使每条指令一次至少处理8个m或n。输入、输出的数据类型均为half时，每个寄存器存储的数据个数nk=2，4个thread总共存储的k=8。一条mma指令一次处理8个m和n时，产生8*8=64个结果，每个thread存储的结果个数为2，使用的寄存器个数为1。

        当一个warp完成M=64，N=64，K=128的乘法时，通用方法是将步长k设置为8，逐步加载M、N，计算乘积，并保存M*N个结果。当一条mma指令一次只能处理8个m和n时，需要对M、N进行切块，M和N的切块个数分别为TileM=M/8=8，TileN=N/8=8，每个thread使用的寄存器个数分别为A=TileM*1=8、B=TileN*1=8、C=TileM*TileN*1=64。存储数据用的寄存器总数为8+8+64=80。这是一个通用方法的简略描述，实际使用时会用更复杂的操作步骤，来提高性能，具体的内容可以在cuda-samples的cudaTensorCoreGemm等示例中查看。

        在4个thread中存储完整的m、n时，每个thread要使用的寄存器个数为K/nk/4=16。当M有多个切块时，使用的寄存器个数为K/nk/4*TileM=128。N可以使用最小值8逐步加载，使用的寄存器个数为K/nk/4=16，存储结果的寄存器个数 C=TileM*1*1=8。存储数据用的寄存器总数为128+16+8=152。通过调节TileM的大小，可以适用不同的较小的K值，从而使查询数据M常驻寄存器。

使查询数据M常驻寄存器有如下优点：
使数据加载指令数减半，每次只需要加载数据库的数据N即可；
提高各级cache的利用率，cache中只需存储N和结果相关的数据；
不需要同步操作，可以让不同warp的计算指令与过滤指令并发执行，现有的通用方法在加载M、N数据时，需要进行同步，才能有比较好的加载效率。

3.结果与讨论

        RTX 2080ti是Nvidia Turning架构的GPU，RTX 3060是Nvidia Ampere架构的GPU，这两款GPU均可以使用TensorCore进行矩阵计算加速。cuBLAS是Nvidia提供的加速矩阵计算的函数库，包含cublasHgemm、cublasSgemmEx、cublasGemmEx等函数，这些函数的输入、输出类型，以及在RTX 2080ti、RTX 3060上的理论算力（单位：TFLOPS）如下表：

函数名称 输入 输出 RTX 2080ti 算力 RTX 3060 算力
cublasSgemmEx half float 53.8 25.6
cublasHgemm half half 107.6 51.2
cublasGemmEx int8 int 215.2 102.4

表3

        Faiss是Facebook开源的用于高效相似性搜索和密集向量聚类的库，我们测试的版本是v1.7.1。其中的Flat算法使用cublasSgemmEx函数进行矩阵计算加速，并通过专门优化过的排序函数排序。

        我们测试了以上函数，以及我们实现的knn搜索函数（输入、输出与cublasHgemm、cublasSgemmEx相同），在K值为128～1024时的效率。距离计算方式为内积时，算力=2MNK/耗时，其中knn搜索的耗时包含排序的时间。knn搜索默认使用的TopK为16，Faiss的Flat算法使用的TopK为1，并且专门测试了TopK为1～1024时两个算法的效率。我们的knn搜索算法使用与表2相同的方式增加过滤目标数、更新阈值。

        我们使用的排序算法是双调排序，代码参考cuda-samples的bitonicSort算法。我们对排序算法做了2处改进：排序过程实际是过滤出的新数据和旧数据的合并过程，旧数据是排序过的数据，所以不需要重复排序；当过滤出的数据多于目标数据时，参与排序的数据量大于要求的数量，此时只需保证要求数量的排序结果准确，超出部分不需进行完整的排序。

        Deep1B[5]是big ann benchmarks使用的数据集之一，我们同样使用它作为主数据集，它的默认维度是96，数据类型float。我们将它作为各种维度的数据来源，如连续读取128、256个float数据，转换为half类型或者量化为int8类型，然后作为128、256维度的数据使用。这样处理会导致这些数据失去本身的含义，但这样做对单纯的性能测试没有影响。我们同样测试了其它的一些数据集，如gist、glove等。

Figure 1：通过以上测试结果可以看到，在K值较低时我们的算法也有很高的硬件利用率，当查询数据可以常驻寄存器时利用率更高。

        使用Nsight Compute工具对计算与过滤函数进行性能分析，2080ti的硬件利用率最高为91.53%，此时TensorCore利用率为86.94%，3060的硬件利用率与TensorCore利用率相同，最高为96%。在分析工具的Pipe Shared Cycles Active的提示中可以看到，2080ti的fp16与tensor共享一个pipe，导致过滤指令和计算指令产生竞争，这可能是TensorCore的利用率低于硬件利用率的原因。由于欧氏距离需要对矩阵乘法的结果做进一步的计算，才能转换为距离，因此编译出的程序和内积距离有较大差异，这些差异导致部分维度时欧式距离的计算效率更高。

        在对M个查询数据进行搜索的过程中，每个分段均会产生M组过滤结果，每组结果的个数为x，M个x组合成集合X，x的平均值近似等于过滤目标数。对集合X进行分析后得到如下结果：随机变量x服从自由度为tk的卡方分布，其中tk近似等于过滤目标数，与数据维度等参数无关。卡方分布是一种特殊的Gamma分布，此时Gamma分布的形状参数α=tk/2、尺度参数β=2。

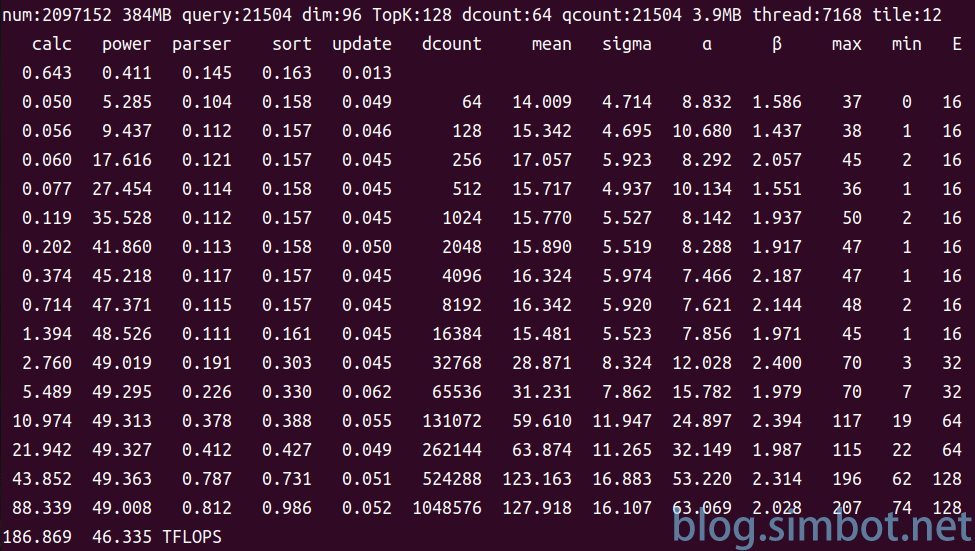
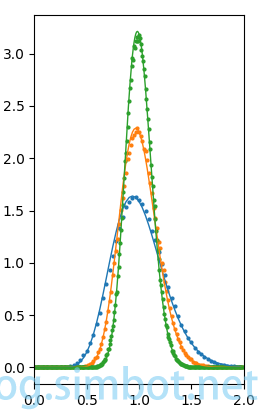Figure 2：上部截图为搜索算法的一张执行截图，数据库大小209万，查询量21504，数据维度96，数据类型half，TopK为128，循环16次结束。第1、2列是距离计算与过滤函数的执行时间（单位：ms）和相应算力（单位：TFLOPS）；第3、4、5列分别是结果解析函数、排序函数、阈值更新函数的执行时间；第6列是分段大小；第7、8列是过滤结果数的均值和标准差；第9、10列是由均值、标准差计算出的Gamma分布的形状参数α、尺度参数β；第11、12列是过滤结果数的最大值、最小值；第13列是过滤目标数。最后一行是整个查询的耗时和相应算力。

Figure 3：左侧蓝色实线是tk=32的概率密度曲线，蓝色圆点是目标数为32的过滤结果数的统计值；橙色实线是tk=64的概率密度曲线，橙色圆点是目标数为64的过滤结果数的统计值；绿色实线是tk=128的概率密度曲线，绿色圆点是目标数为128的过滤结果数的统计值。

        由于首个分段是完整的输出、排序，并存储到结果队列，因此结果队列永不为空，所以初始过滤目标数范围内的召回率为1。当使用表2的方式增加过滤目标数时，由于多个矫正分段的存在，使TopK的召回率也接近于1。可以通过结果队列的填充情况推算召回率，当填充位置达到或超过TopK时，召回率为1。通过控制过滤的结果数，可以减小输出带宽，同时也减小了排序的次数和每次排序的计算量，使硬件的性能得到充分利用。

        Felix Chern等人在Google TPU上实现了峰值性能的knn搜索方法[7]，核心方法也是对结果进行过滤，不过他们没有使用迭代更新阈值的策略，而是通过召回率来控制过滤结果的数量，消除了迭代、排序的开销。他们对内存瓶颈、指令瓶颈做了很详细的分析。

4.结论

        虽然GPU有很高的理论算力，但很少有应用能将其充分利用起来。在本文中，我们提出了一套以过滤为基础的算法，通过对输出结果进行过滤，减少输出带宽，提高硬件利用率；通过对过滤结果数量的控制，提高排序速度，但几乎不影响召回率；通过专门针对低维度计算的优化，使新硬件的利用率达到96%。

本文的部分内容来自我的blog[9]和专利。
Ding Nan[4]、英伟达[10]等对GPU的内存瓶颈、指令瓶颈也有很详细的分析。

参考文献

[1] Jia, Zhe, et al. “Dissecting the NVidia Turing T4 GPU via microbenchmarking.” arXiv preprint arXiv:1903.07486 (2019).

[2] Ebrahimpour, Hossein, and Abbas Kouzani. “Face recognition using bagging KNN.” International conference on signal processing and communication systems (ICSPCS’2007) australia, gold coast. sn, 2007.

[3] Gordo, Albert, et al. “Deep image retrieval: Learning global representations for image search.” European conference on computer vision. Springer, Cham, 2016.

[4] Ding, Nan, and Samuel Williams. “An instruction roofline model for gpus.” 2019 IEEE/ACM Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems (PMBS) (2019): 7-18.

[5] Babenko, Artem, and Victor Lempitsky. “Efficient indexing of billion-scale datasets of deep descriptors.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016.

[6] Johnson, Jeff, Matthijs Douze, and Hervé Jégou. “Billion-scale similarity search with gpus.” IEEE Transactions on Big Data 7.3 (2019): 535-547.

[7] Chern, Felix, et al. “Tpu-knn: K nearest neighbor search at peak flop/s.” arXiv preprint arXiv:2206.14286 (2022).

[8] Kerr, Andrew, et al. “Cutlass: Fast linear algebra in cuda c++.” NVIDIA Developer Blog (2017).

[9] hws000. “The fastest knn search algorithm” https://blog.simbot.net/2022/03/12/the-fastest-knn-search-algorithm/

[10] “Matrix Multiplication Background User’s Guide” NVIDIA Documentation Center https://docs.nvidia.com/deeplearning/performance/dl-performance-matrix-multiplication/index.html

[11] “Matrix multiply-accumulate operation using mma instruction” NVIDIA Documentation Center https://docs.nvidia.com/cuda/parallel-thread-execution/index.html#warp-level-matrix-instructions-for-mma